Video

Mari kita lihat video materi matematika yang edukatif dan menarik di menu sebelah kanan

Profil

BAB VII : PENGELOLAAN DATA

BAB VI : SISTEM KOORDINAT

BAB V : PECAHAN

BAB IV : PENGUMPULAN DAN PENYAJIAN DATA

BAB III : BANGUN DATAR dan BANGUN RUANG

BAB II SATUAN VOLUME dan DEBIT

BAB I : BILANGAN BULAT

PROGRAM TAHUNAN KELAS 6

Power Point Materi Matematika kelas 6

BAB I : BILANGAN BULAT BAB II : SATUAN VOLUME DAN DEBIT BAB III : LUAS BANGUN DATAR DAN VOLUME BANGUN RUANG BAB IV : PENYAJIAN DAN PENGOLAHAN DATA BAB V : PECAHAN BAB VI : SISTEM KOORDINAT BAB VII : PENGELOLAAN DATA

BAB II : SATUAN VOLUME dan DEBIT

BAB I : BILANGAN BULAT

PENGELOLAAN DATA

Menyajikan Data

1. Menyajikan Data dalam Bentuk Tabel 

Siswa Kelas VI sedang melaksanakan ulangan Matematika. Setelah diperiksa, dari 40 siswa diperoleh hasil ulangan setiap siswa adalah sebagai berikut.
6, 8, 6, 7, 5, 9, 6, 7, 5, 7 9, 7, 5, 8, 6, 7, 7, 6, 9, 6
 9, 7, 7, 6, 6, 8, 5, 7, 9, 8 8, 9, 7, 8, 7, 9, 6, 7, 8, 8
Berapa banyak siswa yang memperoleh nilai 6? Berapa banyak siswa yang memperoleh nilai 8? Agar lebih mudah menjawabnya, maka kumpulan data hasil ulangan Matematika tersebut dapat disajikan dalam bentuk tabel berikut ini.

Dari tabel tersebut, kamu dapat melihat bahwa siswa yang memperoleh nilai 5 sebanyak 4 orang. Siswa yang memperoleh nilai 6 sebanyak 9 orang. Siswa yang memperoleh nilai 7 sebanyak 12 orang. Siswa yang memperoleh nilai 8 sebanyak 8 orang, dan siswa yang memperoleh nilai 9 sebanyak 7 orang.

2. Menyajikan Data dengan Diagram Gambar
Kumpulan data nilai ulangan Matematika dari 40 siswa Kelas VI dapat juga disajikan menggunakan diagram gambar berikut ini.

     Diagram seperti ini dinamakan diagram gambar atau piktogram. Diagram tersebut menggunakan gambar orang untuk menyatakan jumlah siswa. Satu gambar mewakili 1 orang siswa. Dengan demikian, banyak siswa yang memperoleh nilai 5 ada 4 orang, siswa yang memperoleh nilai 6 ada 9 orang, dan seterusnya

Menentukan Rata-Rata dan Modus

SISTEM KOORDINAT

Membaca dan Membuat Denah Letak Benda

 Dari denah tersebut, kamu dapat memperoleh informasi berikut.

 1. Sebelah timur Kantor Kelurahan terdapat perumahan penduduk. 

2. Puskesmas terletak di sebelah barat perkebunan kelapa. 

3. Sebelah utara komplek perumahan terdapat perkebunan kelapa dan sekolah. 

4. Jembatan terletak di sebelah selatan pesawahan.

Koordinat

1. Koordinat Letak Benda
1. Gambar topi terletak pada kotak pertemuan antara angka 1 dan huruf A, ditulis (1, A).
2. Gambar jam terletak pada kotak pertemuan antara angka 2 dan huruf C, ditulis (2, C).
3. Gambar kamera terletak pada kotak pertemuan antara angka 4 dan huruf B, ditulis (4, B).
Coba kamu tentukan di mana posisi radio, TV, dan buku.
Pasangan angka dan huruf (1, A); (2, C); (4, B) dinamakan koordinat. 

Koordinat adalah bilangan yang dipakai untuk menunjukkan lokasi suatu titik di garis permukaan atau ruang. Koordinat dapat memudahkan kita dalam menemukan letak benda.

2. Koordinat Letak Tempat pada Peta

 Berdasarkan peta tersebut, kamu dapat memperoleh informasi berikut ini. 

1. Kota Banawa terletak pada koordinat (2, H). 

2. Kota Poso terletak pada koordinat (4, F). 

3. Kota Luwuk terletak pada koordinat (9, G). 

4. Pulau Menul terletak pada koordinat (10, A). 

5. Kota Bungku terletak pada koordinat (7, C).

Sistem Koordinat Kartesius

Gambar tersebut disebut Koordinat Kartesius. Sistem Koordinat Kartesius terdiri atas sumbu mendatar (sumbu-x) dan sumbu tegak (sumbu-y). Fungsi kedua sumbu tersebut adalah untuk menentukan letak suatu titik. Titik-titik pada koordinat Kartesius merupakan pasangan titik pada sumbu-x dan sumbu-y (x, y). Di mana x disebut absis dan y disebut ordinat. Perpotongan antara sumbu-x dan sumbu-y di titik 0 (nol) disebut pusat koordinat. Berdasarkan sistem koordinat Kartesius tersebut kamu dapat memperoleh informasi berikut ini. 

1. Titik A terletak pada koordinat (1, 3). 

2. Titik B terletak pada koordinat (0, 4). 

3. Titik C terletak pada koordinat (–2, 1). 

4. Titik D terletak pada koordinat (4, –2). 

5. Titik E terletak pada koordinat (2, –4)

Menggambar Bangun Datar pada Bidang Koordinat

Gambarlah olehmu titik A(2, 2), B(7, 2), C(7, 5), dan D (2, 5). 

Kemudian, hubungkan titik A, B, C, dan D dengan garis.

Bangun apakah yang terbentuk? 

Dapatkah kamu menentukan luas dari bangun tersebut? 

Selanjutnya, gambarlah titik E(3, –2), F(3, –5), dan G(5, –5). 

Kemudian, hubungkan titik E, F, sampai G dengan garis. 

Bangun apakah yang terbentuk? Bagaimana cara menghitung luas bangun yang terbentuk tersebut? 

Bangun ABCD yang terbentuk pada koordinat Kartesius tersebut adalah persegi panjang.

Panjang AB = 5 satuan panjang dan panjang AD = 3 satuan panjang. 

Luas daerah persegipanjang ABCD = 5 × 3 = 15 satuan luas. 

Adapun bangun EFG adalah segitiga. 

Panjang EF = 3 satuan panjang dan panjang FG = 2 satuan   panjang.

 Dengan demikian, luas daerah segitiga EFG = 1 2 × 3 × 2 = 3 satuan luas.

PECAHAN

Mengubah Pecahan Menjadi Pecahan yang Senilai 

Menyederhanakan Pecahan

Mengurutkan Pecahan

                   Untuk mengurutkan bilangan cacah seperti 10, 8, 15, 6, 20, mulai dari yang terkecil mungkin kamu lebih mudah mengurutkannya, yaitu 6, 8, 10, 15, 20. Akan tetapi, untuk mengurutkan bilangan pecahan, apalagi pecahan yang tidak sejenis kamu perlu mempelajari langkah-langkahnya. Dalam mengurutkan pecahan, hal pertama yang harus dilakukan adalah memperhatikan penyebutnya. 

Jika penyebutnya sama, urutkan pecahan-pecahan tersebut dari yang pembilangnya terkecil sampai dengan yang terbesar atau sebaliknya.

 Jika penyebutnya tidak sama, samakan dahulu penyebut pecahan-pecahan tersebut dengan menggunakan KPK dari penyebut-penyebut tersebut. Setelah itu, urutkan pecahan-pecahan tersebut dari yang pembilangnya terkecil sampai dengan yang terbesar atau sebaliknya.

Mengubah Bentuk Pecahan Menjadi Bentuk Desimal

1. Mengubah Pecahan Biasa Menjadi Bentuk Desimal 

 2. Mengubah Pecahan Campuran Menjadi Bentuk Desimal

3. Mengubah Bentuk Persen Menjadi Bentuk Desimal

4. Mengubah Bentuk Pecahan Menjadi Bentuk Persen

 

 

PENGUMPULAN dan PENYAJIAN DATA

Mengumpulkan dan Menyajikan Data

1. Mengumpulkan Data dengan Cara Pencatatan Langsung

       Siswa Kelas VI yang berjumlah 30 orang telah selesai melaksanakan ulangan Matematika. Kemudian, ibu guru memeriksanya dan mencatat hasil ulangan Matematika setiap siswa sebagai berikut. 

6, 6, 7, 7, 8, 5, 9, 7, 6, 7 8, 8, 8, 6, 5, 6, 6, 7, 9, 6 7, 7, 8, 8, 7, 8, 9, 9, 7, 5

        Ibu guru ingin mengelompokkan nilai yang diperoleh setiap siswa tersebut. Ada berapa orang yang mendapat nilai 7? Ada berapa orang yang mendapat nilai 8? dan seterusnya.

2. Mengumpulkan Data dengan Cara Mengisi Lembar Isian

        Siswa Kelas VI akan mengadakan pemilihan ketua kelas. Dari 40 siswa, telah terpilih calon-calon yang akan menjadi ketua kelas, di antaranya Andi, Ika, Santi, dan Rudi. Kemudian, beberapa orang siswa membuat lembar isian untuk dibagikan dan diisi oleh setiap siswa. Lembar isian itu tampak seperti berikut.

 Setelah dikumpulkan, data-data tersebut dicatat di papan tulis dan diperoleh hasil sebagai berikut.

      Dari hasil tersebut ternyata sebanyak 16 siswa memilih Ika, 10 siswa memilih Andi, 8 siswa memilih Santi, dan 6 siswa memilih Rudi. Akhirnya Ika yang terpilih menjadi ketua kelas karena memperoleh suara yang terbanyak. Contoh pemilihan ketua kelas ini merupakan pengumpulan data dengan cara menggunakan lembar isian.

Menafsirkan Data 

1. Menafsirkan Data Berbentuk Diagram Batang

 Perhatikan diagram batang yang menunjukkan hasil ulangan Matematika dari 30 orang siswa.

 Dari diagram tersebut, dapat dilihat bahwa:

 a. Siswa yang mendapat nilai 5 ada 3 orang.

 b. Siswa yang mendapat nilai 6 ada 7 orang. 

c. Siswa yang mendapat nilai 7 ada 9 orang. 

d. Siswa yang mendapat nilai 8 ada 7 orang. 

e. Siswa yang mendapat nilai 9 ada 4 orang. 

Dari tabel tersebut terlihat juga bahwa jumlah siswa yang mendapat nilai 6 dan 8 adalah sama, yaitu 7 siswa. Nilai berapakah yang paling banyak diperoleh siswa? Ada berapa siswa yang mendapat nilai paling tinggi?

2. Menafsirkan Data Berbentuk Diagram Lingkaran 

       Selain diagram batang, diagram lingkaran juga sering digunakan dalam kehidupan sehari-hari. Misalnya data mengenai warna yang paling disukai oleh 40 siswa Kelas VI disajikan sebagai berikut. Bagaimana cara membaca diagram lingkaran ini? Berapa banyak siswa yang menyukai warna merah? Berapa banyak siswa yang menyukai warna abu-abu? Agar dapat membaca diagram tersebut, lakukan perhitungan berikut.

 Dengan demikian, sebanyak 12 siswa menyukai warna merah dan 7 orang siswa menyukai warna abu-abu.

Besar sudut satu putaran penuh adalah 360°.
Untuk menentukan besar sudut pada bagian yang berwarna merah dan kuning, kamu dapat menghitungnya sebagai berikut.
Besar sudut bagian yang berwarna merah adalah
= 30% × 360° = 30/ 100 x 360° = 3 / 10 x 360° = 1.080 / 10  = 108°.
Besar sudut yang berwarna kuning adalah
= 10% × 360° = 10/ 100 x 360° =1 /10x 360° = 360°/10=36°

 

LUAS BANGUN DATAR dan VOLUME BANGUN RUANG

LUAS BANGUN DATAR 

 1. Mengingat Kembali Luas Persegi, Persegipanjang, Segitiga, Jajargenjang, dan Trapesium 

      Untuk mengingat kembali bagaimana menghitung luas persegi, persegipanjang, segitiga, jajargenjang, dan trapesium, perhatikan contoh berikut.

 Jawab:
a. Luas persegi ABCD = s × s
                                     = 5 cm × 5 cm
                                     = 25 cm2
    Jadi, luas persegi ABCD adalah 25 cm2 .
b. Luas persegipanjang EFGH = p ×l
                                                 = 10 cm × 5 cm
                                                 = 50 cm2
   Jadi, luas persegipanjang EFGH adalah 50 cm2 .
c. Luas segitiga KLM = 1 2 × (a × t)
                                    = 1 2 × (12 cm × 6 cm)
                                    = 1 2 × 72 cm2
                                    = 36 cm2
   Jadi, luas segitiga KLM adalah 36 cm2 .

2. Menghitung Luas Segi Banyak
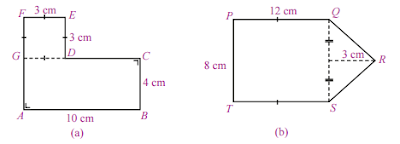
   Ayo, perhatikanlah gambar berikut.

 

Bangun datar pada Gambar (a) dan (b) dinamakan juga segi banyak. Bangun (a) dibentuk oleh persegipanjang dan persegi. Adapun bangun (b) dibentuk oleh persegipanjang dan segitiga. Bagaimanakah cara menghitung luas segi banyak tersebut?

 Langkah-langkah untuk menghitung luas segi banyak adalah sebagai berikut. 

1. Tentukan bangun datar apa saja yang membentuknya. 

2. Tentukan luas dari setiap bangun datar yang membentuknya. 

3. Jumlahkan luas dari keseluruhan bangun datar yang membentuknya 

Berdasarkan langkah-langkah tersebut, maka

 • Luas bangun (a) = luas persegipanjang ABCG + luas persegi DEFG 

                              = (10 cm × 4 cm) + (3 cm × 3 cm) 

                              = 40 cm2 + 9 cm2 = 49 cm2 

• Luas bangun (b) = luas persegipanjang PQST + luas segitiga QRS 

                              = (12 cm × 8 cm) + ( 1 2 × 8 cm × 3 cm) 

                              = 96 cm2 + 12 cm2 

                              = 108 cm2

3. Menghitung Luas Lingkaran

a. Jari-jari dan Diameter Lingkaran 

Perhatikanlah gambar lingkaran dengan titik pusat O berikut. 

           Jarak dari titik pusat ke setiap titik pada lingkaran dinamakan jari-jari lingkaran. Pada gambar tersebut jarak titik O ke titik A sama dengan jarak titik O ke titik B yang dalam hal ini merupakan jari-jari lingkaran. Jari-jari lingkaran biasanya dilambangkan dengan r. Diameter lingkaran adalah panjang ruas garis lurus yang melalui titik pusat dan menghubungan dua buah titik pada lingkaran. Sebagai contoh, perhatikan gambar lingkaran berikut ini. 

         Titik pusat lingkaran pada gambar di atas adalah O. Titik A, B, C, dan D ada pada lingkaran. Ruas garis AC dan BD melalui titik O. Panjang ruas garis AC sama dengan ruas garis BD yang merupakan diameter lingkaran tersebut. Diameter lingkaran dilambangkan dengan d. Diameter lingkaran sama dengan dua kali jari-jarinya. Dengan demikian,

 d = 2 × r

b. Keliling Lingkaran

          Sebuah taman berbentuk lingkaran memiliki diameter 5 meter. Ali berlari mengelilingi taman itu satu kali putaran. Berapa meter jarak yang telah ditempuh Ali? Jarak yang ditempuh Ali sama dengan keliling taman yang berbentuk lingkaran tersebut. Dapatkah kamu mencari keliling lingkaran jika diketahui diameternya? 

Perbandingan keliling (K) dan diameter lingkaran (d) mendekati bilangan 3,14 atau 22/ 7 . Selanjutnya, bilangan ini dinamakan π , dibaca pi .

 Bangun Ruang

1. Menghitung Volume Prisma Tegak Segitiga

2. Menghitung Volume Tabung

 

SATUAN VOLUME DAN DEBIT

SATUAN VOLUME 

1. Hubungan Antar Satuan Volume

   Volume kubus dengan panjang rusuk 1 cm adalah 

   V = 1 cm × 1 cm × 1 cm = (1 × 1 × 1) cm3 = 1 cm3 . 

   Volume kubus dengan panjang rusuk 10 mm adalah

   V = 10 mm × 10 mm × 10 mm = (10 × 10 × 10) mm3 = 1.000 mm3 . 

   Jadi, 

 Volume kubus dengan panjang rusuk 1 dm adalah 

 V = 1 dm × 1 dm × 1 dm = (1 × 1 × 1) dm3 = 1 dm3 . 

 Volume kubus dengan panjang rusuk 10 cm adalah 

  V = 10 cm × 10 cm × 10 cm = (10 × 10 × 10) cm3 = 1.000 cm3 . 

  Jadi,

Contoh-contoh tersebut menggambarkan hubungan antara satuan volume cm3 dan mm3 , juga antara satuan dm3 dan cm3 . Hubungan antar satuan volume lainnya, dapat kamu pelajari sebagai berikut. Perhatikan gambar hubungan antar satuan kubik berikut.

Contoh 

 a. 2 m3 = ... dm3 

 b. 6.000 cm3 = ... dm3 

Jawab: 

 a. 2 m3 = (2 × 1) m3 

             = (2 × 1.000) dm3 

             = 2.000 dm3 

 b. 6.000 cm3 = (6.000 × 1) cm3 

                       = (6.000 : 1.000) dm3 

                       = 6 dm3

2. Satuan Liter dan Mililiter
Dalam kehidupan sehari-hari satuan volume yang sering digunakan adalah liter (l) dan mililiter (ml). Misalnya, volume minuman ringan ini adalah 1 liter. Berapa mililiterkah volume minuman ringan ini? 

Ingatlah kembali tentang hubungan antar satuan panjang. 
Satu milimeter sama dengan 1 /1.000 meter. Begitu juga dalam satuan volume, 1 mililiter sama dengan 1/1.000 liter. Oleh karena itu, 1 mililiter = 1 /1.000 liter atau 1 liter = 1.000 ml. Satu liter sama dengan 1 dm3 , dan 1 mililiter sama dengan 1 cm3 . 

Contoh
 a. 4 l = ... ml
b. 7.000 ml = ...
Jawab:
a. 4 l  = (4 × 1)
          = (4 × 1.000) ml
          = 4.000 ml
          (Karena 1 l = 1.000 ml)
b. 7.000 ml = (7.000 × 1) ml
                   = (7.000 : 1.000) l
                   = 7 l 

SATUAN DEBIT

 1. Arti Satuan Debit 
          Ira akan mengisi sebuah ember dengan air dari keran. Dalam waktu 1 menit, ember tersebut   terisi 6 liter air. Artinya, debit air yang mengalir dari keran itu adalah 6 liter/menit, ditulis 6 l /menit.

           Satuan debit biasanya digunakan untuk menentukan volume air yang mengalir dalam suatu satuan waktu.

Contoh:
1.  Sebuah kolam diisi air dengan menggunakan pipa yang debitnya 1 l/detik. Artinya, dalam waktu   1   detik volume air yang mengalir dari pipa tersebut adalah 1 liter.

2. Debit air yang mengalir pada pintu air Manggarai adalah 500 m3 /detik. Artinya, dalam waktu 1 detik volume air yang mengalir melalui pintu air Manggarai adalah 500 m3 .

2. Hubungan Antar Satuan Debit
           Satuan debit yang sering digunakan adalah l/detik dan m3 /detik.
1 l = 1 dm3 = 1 / 1.000 m3 . Oleh karena itu,

 Contoh
 a. 4 m3 /detik = ... l/detik
 b. 6.000 l/detik = ... m3 /detik
Jawab:
 a. 4 m3 /detik = (4 × 1) m3 /detik
                       = (4 × 1.000) l/detik
                       = 4.000 l/detik
 b. 6.000 l/detik = (6.000 × 1) l/detik
                          = (6.000 : 1.000) m3 /detik
                          = 6 m3 /detik

BILANGAN BULAT

Sifat-Sifat Operasi Hitung 

1. Sifat Komutatif 

 Seperti yang telah kamu ketahui, sifat komutatif disebut juga sifat pertukaran.
 Untuk lebih jelasnya, perhatikan penjumlahan berikut! 

 2 + 4 = 6                4 + 2 = 6 

Jadi, 2 + 4 = 4 + 2

Sifat seperti ini dinamakan sifat komutatif pada penjumlahan. 

Sekarang, coba perhatikan perkalian berikut! 

2 × 4 = 8           4 × 2 = 8 

Jadi, 2 × 4 = 4 × 2. 

Sifat seperti ini dinamakan sifat komutatif pada perkalian. 

Apakah sifat komutatif berlaku pada pengurangan dan pembagian? 

Perhatikan contoh berikut!
 a. 2 – 4 = –2   dan    4 – 2 = 2
     Jadi, 2 – 4 tidak sama dengan 4 – 2,
     atau
      2 – 4 ≠ 4 – 2.
b. 2 : 4 = 0,5 dan  4 : 2 = 2
     Diperoleh bahwa 2 : 4 tidak sama dengan 4 : 2, atau 2 : 4 ≠ 4 : 2



2. Sifat Asosiatif

 Pada penjumlahan dan perkalian tiga bilangan bulat berlaku sifat asosiatif atau disebut juga sifat  pengelompokan.

 Perhatikanlah contoh penjumlahan tiga bilangan berikut!

(2 + 3) + 4 = 5 + 4 = 9 

2 + (3 + 4) = 2 + 7 = 9

 Jadi, (2 + 3) + 4 = 2 + (3 + 4). 

 Sifat seperti ini dinamakan sifat asosiatif pada penjumlahan. 

 Sekarang, coba perhatikan contoh perkalian berikut!

(2 × 3) × 4 = 6 × 4 = 24 

2 × (3 × 4) = 2 × 12 = 24

 Jadi, (2 × 3) × 4 = 2 × (3 × 4). 

 Sifat ini disebut sifat asosiatif pada perkalian. 

3. Sifat Distributif 

 Selain sifat komutatif dan sifat asosiatif, terdapat pula sifat distributif.  Sifat distributif disebut juga sifat penyebaran.  Untuk lebih memahaminya, perhatikanlah contoh berikut. 
Contoh                                    Apakah 3 × (4 + 5) = (3 × 4) + (3 × 5)? 

Jawab: 3 × (4 + 5) = 3 × 9 = 27

 (3 × 4) + (3 × 5) = 12 + 15 = 27 

Jadi, 3 × (4 + 5) = (3 × 4) + (3 × 5). 

 4. Menggunakan Sifat-Sifat Operasi Hitung 

Sifat distributif dapat kamu gunakan pada perkalian dua bilangan. Pada perkalian tersebut, salah satu bilangannya merupakan bilangan yang cukup besar.  Agar kamu lebih memahaminya, coba pelajari contoh-contoh berikut. 
Contoh 
 a. 8 × 123 = ...
 b. 6 × 98 = ...
Jawab: 
a. 8 × 123 = 8 × (100 + 20 + 3)
                 = (8 × 100) + (8 × 20) + (8 × 3) 
                 = 800 + 160 + 24 = 984
    Jadi, 8 × 123 = 984.
b. 6 × 98 = 6 × (100 – 2) 
               = (6 × 100) – (6 × 2) 
               = 600 – 12 = 588 
    Jadi, 6 × 98 = 588. 

Menentukan FPB dan KPK

1. Menentukan FPB

    Langkah-langkah pengerjaan FPB. 

    1. Menentukan faktorisasi prima dari bilangan-bilangan itu. 

    2. Mengambil faktor yang sama dari bilangan-bilangan itu. 

    3. Jika faktor yang sama pangkatnya berbeda, ambillah faktor yang pangkatnya terkecil. 

    Perhatikan diagram berikut ini. 

    Faktorisasi prima dari 12 adalah 12 = 2 × 2 × 3 = 22 × 3.

    Faktorisasi prima dari 18 adalah 18 = 2 × 3 × 3 = 2 × 32 . 

    FPB dari 12 dan 18 adalah 2 × 3 = 6. 

    Jadi, kantong plastik yang diperlukan adalah 6 buah. 

    Setiap kantong plastik memuat 2 apel dan 3 jeruk, 

   seperti terlihat pada gambar berikut. 

2. Menentukan KPK

    Langkah-langkah menentukan KPK. 

    1. Tentukan faktorisasi prima dari bilangan-bilangan tersebut. 

    2. Ambil semua faktor yang sama atau tidak sama dari bilangan-bilangan tersebut. 

    3. Jika faktor yang sama memiliki pangkat berbeda, ambillah faktor yang pangkatnya terbesar.

   Faktorisasi prima dari 12 adalah 12 = 2 × 2 × 3 = 22 ×3. 

   Faktorisasi prima dari 18 adalah 18 = 2 × 3 × 3 = 2 × 32 . 

   KPK dari 12 dan 18 adalah 22 × 32 = 4 × 9 = 36.

Perpangkatan dan Penarikan Akar Pangkat Tiga

1. Perpangkatan Tiga 

Jika suatu bilangan dikalikan dengan dirinya sendiri, dikatakan bahwa bilangan tersebut dikuadratkan. 

Misalnya, 5 × 5 = 25, dapat ditulis 52 = 25. 

Artinya, kuadrat dari 5 adalah 25. 

Adapun 25 disebut bilangan kuadrat. 

 Dengan cara yang sama, kamu dapat memahami perpangkatan tiga dari suatu bilangan. 

Misalnya, 5 × 5 × 5 = 125, dapat ditulis 53 =125.

2. Penarikan Akar Pangkat Tiga

3. Operasi Hitung pada Bilangan Berpangkat

Operasi hitung seperti penjumlahan, pengurangan, perkalian, dan pembagian dapat juga dilakukan pada bilangan berpangkat maupun bilangan akar. Agar lebih jelas, pelajari contoh-contoh berikut.