Serba Serbi Matematika 6 MI: LUAS BANGUN DATAR dan VOLUME BANGUN RUANG

LUAS BANGUN DATAR

1. Mengingat Kembali Luas Persegi, Persegipanjang, Segitiga, Jajargenjang, dan Trapesium

Untuk mengingat kembali bagaimana menghitung luas persegi, persegipanjang, segitiga, jajargenjang, dan trapesium, perhatikan contoh berikut.

Jawab:
a. Luas persegi ABCD = s × s
   = 5 cm × 5 cm
                                     = 25 cm2
    Jadi, luas persegi ABCD adalah 25 cm2 .
b. Luas persegipanjang EFGH = p ×l
                                                 = 10 cm × 5 cm
                                                 = 50 cm2
   Jadi, luas persegipanjang EFGH adalah 50 cm2 .
c. Luas segitiga KLM = 1 2 × (a × t)
                                    = 1 2 × (12 cm × 6 cm)
                                    = 1 2 × 72 cm2
                                    = 36 cm2
   Jadi, luas segitiga KLM adalah 36 cm2 .

2. Menghitung Luas Segi Banyak
   Ayo, perhatikanlah gambar berikut.

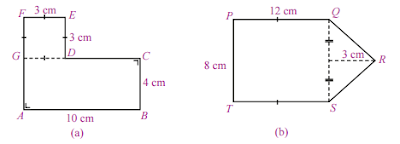
Bangun datar pada Gambar (a) dan (b) dinamakan juga segi banyak. Bangun (a) dibentuk oleh persegipanjang dan persegi. Adapun bangun (b) dibentuk oleh persegipanjang dan segitiga. Bagaimanakah cara menghitung luas segi banyak tersebut?

Langkah-langkah untuk menghitung luas segi banyak adalah sebagai berikut.

1. Tentukan bangun datar apa saja yang membentuknya.

2. Tentukan luas dari setiap bangun datar yang membentuknya.

3. Jumlahkan luas dari keseluruhan bangun datar yang membentuknya

Berdasarkan langkah-langkah tersebut, maka

• Luas bangun (a) = luas persegipanjang ABCG + luas persegi DEFG

= (10 cm × 4 cm) + (3 cm × 3 cm)

= 40 cm2 + 9 cm2 = 49 cm2

• Luas bangun (b) = luas persegipanjang PQST + luas segitiga QRS

= (12 cm × 8 cm) + ( 1 2 × 8 cm × 3 cm)

= 96 cm2 + 12 cm2

= 108 cm2

3. Menghitung Luas Lingkaran

a. Jari-jari dan Diameter Lingkaran

Perhatikanlah gambar lingkaran dengan titik pusat O berikut.

Jarak dari titik pusat ke setiap titik pada lingkaran dinamakan jari-jari lingkaran. Pada gambar tersebut jarak titik O ke titik A sama dengan jarak titik O ke titik B yang dalam hal ini merupakan jari-jari lingkaran. Jari-jari lingkaran biasanya dilambangkan dengan r. Diameter lingkaran adalah panjang ruas garis lurus yang melalui titik pusat dan menghubungan dua buah titik pada lingkaran. Sebagai contoh, perhatikan gambar lingkaran berikut ini.

Titik pusat lingkaran pada gambar di atas adalah O. Titik A, B, C, dan D ada pada lingkaran. Ruas garis AC dan BD melalui titik O. Panjang ruas garis AC sama dengan ruas garis BD yang merupakan diameter lingkaran tersebut. Diameter lingkaran dilambangkan dengan d. Diameter lingkaran sama dengan dua kali jari-jarinya. Dengan demikian,

d = 2 × r

b. Keliling Lingkaran

Sebuah taman berbentuk lingkaran memiliki diameter 5 meter. Ali berlari mengelilingi taman itu satu kali putaran. Berapa meter jarak yang telah ditempuh Ali? Jarak yang ditempuh Ali sama dengan keliling taman yang berbentuk lingkaran tersebut. Dapatkah kamu mencari keliling lingkaran jika diketahui diameternya?

Perbandingan keliling (K) dan diameter lingkaran (d) mendekati bilangan 3,14 atau 22/ 7 . Selanjutnya, bilangan ini dinamakan π , dibaca pi .